개요

AI에 대한 기초를 다시 정리하고자 아래 내용을 읽고 정리했습니다.

• https://wikidocs.net/53560

데이터에 대한 이해 (Data Definition)

모델을 학습시키기 위해선 훈련 데이터셋과 테스트 데이터셋으로 나누어구성합니다.

훈련 데이터셋은 텐서의 형태를 가져야하며 입력과 출력을 구분합니다.

• x(입력) → 모델 → y(출력)

공부한 시간 대비 시험 점수를 예측하는 모델을 만든다고 했을 때 데이터는 다음과 같이 구성됩니다.

x_train = torch.FloatTensor([[1], [2], [3]])
y_train = torch.FloatTensor([[2], [4], [6]])

가설 수립

선형 회귀의 가설은 H(x) = Wx + b 라는 직선의 방정식입니다. 기본적인 직선의 방정식 y = ax + b 와 같은 형식을 가집니다. 따라서 W는 기울기(Weight), b는 편향(절편,bias)라고 표현합니다.

선형 회귀 모델이란건 W와 b 값을 계속 조정해가며 가장 잘 맞는 직선을 찾는 것 입니다.

비용 함수(Cost Function)

가장 잘 맞는 직선을 찾기 위해선 점과 직선 사이의 거리가 최소(오차가 최소)인 직선을 찾는 것과 동일합니다.

좋은 직선이라는 것을 수치적으로 표현하기 위해 오차를 계산해야하는데 오차를 계산하기 위한 함수를 **비용 함수(Cost Function)**이라고 합니다. 비용 함수를 표현하는 용어는 다양합니다.

• 비용 함수(cost function) = 손실 함수(loss function) = 오차 함수(error function) = 목적 함수(objective function)
  • 비용 함수, 손실 함수라는 이름으로 자주 언급 됨.

하지만 실제 계산을 위해선 오차가 -3, +3인 점들이 존재하며 이를 덧셈으로 계산하기엔 오차가 0이되어 없는 것처럼 보이게 됩니다. 이렇게 음수를 없애기 위해 평균 제곱 오차(MSE) 를 사용합니다.

MSE의 수식은 다음과 같습니다.

• (1/n) × Σ(실제값 - 예측값)²
  • 데이터가 많으면 많을수록 오차가 커지는 것을 방지하기 위해 평균을 구합니다.
  • 제곱하기 때문에 오차가 크면 클수록 더 크게 반영됩니다.

옵티마이저 경사 하강법(Gradient Descent)

비용 함수를 통해 비용을 최소로 만드는 W와 b를 찾을 수 있게 되었습니다.

하지만 W와 b의 조합은 무한한만큼 이것들을 모두 대입하며 찾을 수 없습니다.

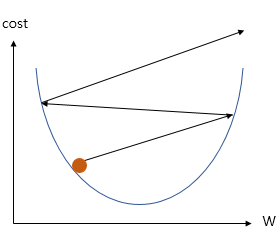
따라서 효율적으로 최소값을 찾기위한 방법이 필요합니다. 이것은 산에서 눈을 가리고 가장 낮은 지점으로 가는 방법과 유사합니다. 우리가 눈을 가렸을 때 가장 낮은 곳으로 이동하기 위해선 기울기(gradient)를 따라 내려가는(desscent) 방향으로 가야합니다.

이것을 경사하강법이라고 하며 수학적으로 함수의 기울기(순간 변화율)를 구합니다. 내려가는 값을 구하기 위해 비용 함수를 미분합니다. 현재 W에서 기울기를 구하고 그 방향으로 내려가게 됩니다. 기울기가 0이 되는 지점(=비용이 최소인 지점)까지 반복합니다.

공식은 다음과 같습니다.

• W := W - α × (기울기)

여기서의 α 는 학습률을 의미합니다. 학습률은 W를 업데이트하는 폭(step)입니다. 학습률이 너무 작으면 최소값을 찾기 위해 조금씩 움직이다보니 정확한 지점을 찾을 수 있겠지만, 학습 과정이 너무 느립니다. 반대로 너무 크면 빠르지만 최소값을 못 찾고 발산할 수 있습니다.

가설과 비용 함수, 옵티마이저는 ML에서 자주 사용되는 포괄적인 개념입니다.

파이토치 선형회귀 구현

기본 설정

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim

# 현재 실습하고 있는 파이썬 코드를 재실행해도 다음에도 같은 결과가 나오도록 랜덤 시드(random seed)를 줍니다.
torch.manual_seed(1)

선형 회귀를 구현하기 위해 파이토치 코드에서는 아래와 같이 선언합니다.

W = torch.zeros(1, requires_grad=True)

requires_grad 는 변수에 대해 기울기를 계산(추적)하겠다는 의미로 사용됩니다. Training 중 반복되어 값이 계산됩니다.

cost.backward()

비용 함수를 미분해서 W에 대한 기울기를 계산합니다.

만약 MSE라면 cost = (1/n) × Σ(y - (Wx + b))² 해당 값을 미분하여 W를 조정합니다.

optimizer.zero_grad()

현재 위치에서 기울기를 다시 조정하기 위해 0으로 초기화합니다.

optimizer.step()

계산된 기울기를 바탕으로 W와 b를 실제 업데이트합니다.

# 데이터
x_train = torch.FloatTensor([[1], [2], [3]])
y_train = torch.FloatTensor([[2], [4], [6]])
# 모델 초기화
W = torch.zeros(1, requires_grad=True)
b = torch.zeros(1, requires_grad=True)
# optimizer 설정
optimizer = optim.SGD([W, b], lr=0.01)

nb_epochs = 1999 # 원하는만큼 경사 하강법을 반복
for epoch in range(nb_epochs + 1):

    # H(x) 계산 → 예측값 계산
    hypothesis = x_train * W + b

    # cost 계산 → 오차(비용) 계산
    cost = torch.mean((hypothesis - y_train) ** 2)

    # cost로 H(x) 개선
    optimizer.zero_grad() # → 기울기 초기화
    cost.backward() # → 오차를 미분해서 기울기 계산
    optimizer.step() # → 기울기로 W, b 업데이트

    # 100번마다 로그 출력
    if epoch % 100 == 0:
        print('Epoch {:4d}/{} W: {:.3f}, b: {:.3f} Cost: {:.6f}'.format(
            epoch, nb_epochs, W.item(), b.item(), cost.item()
        ))

1. 실제 값을 계산하고 오차를 계산합니다. 가설
2. 현재 기울기를 초기화합니다. zero_grad()
3. 오차를 미분하여 기울기를 계산합니다. backward()
4. 계산된 기울기로 W, b 값을 업데이트 합니다. step()
5. … 반복합니다.