개요

AI에 대한 기초를 다시 정리하고자 아래 내용을 읽고 정리했습니다.

• https://wikidocs.net/54841

다중 선형 회귀(Multivariable Linear Regression)

<단순 선형 회귀 차이>

현실 세계에서는 하나의 요소만 결과에 영향을 주지 않습니다. 즉 다양한 요소가 예측에 영향을 주게 되는데 이처럼 여러 입력을 사용하는 것을 다중 선형 회귀라고 표현합니다.

수식은 선형 회귀와 유사합니다. 각 요소별로 가중치(w)가 붙으며 입력되는 변수의 개수에 따라 확장됩니다.

• H(x) = w₁x₁ + w₂x₂ + w₃x₃ + ... + b

기본 구현 (변수 개별 선언)

<기본 설정>

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim

torch.manual_seed(1)

<x1_train, x2_train, x3_train / w1, w2, w3 개별 선언>

훈련 데이터 입력시 x가 1,000개라면 x1_train, x2_train, ... x1000_train , w도 w1, w2, … , w1000으로 작성해야하는 불편함이 존재합니다. 문제를 해결하기 위해 Pytorch에서는 행렬 곱셈 연산을 사용할 수 있습니다.

즉 변수가 많아지면 불편합니다.

# 훈련 데이터
x1_train = torch.FloatTensor([[73], [93], [89], [96], [73]])
x2_train = torch.FloatTensor([[80], [88], [91], [98], [66]])
x3_train = torch.FloatTensor([[75], [93], [90], [100], [70]])
y_train = torch.FloatTensor([[152], [185], [180], [196], [142]])

# 가중치 w와 편향 b 초기화
w1 = torch.zeros(1, requires_grad=True)
w2 = torch.zeros(1, requires_grad=True)
w3 = torch.zeros(1, requires_grad=True)
b = torch.zeros(1, requires_grad=True)

<행렬 연산으로 개선하기>

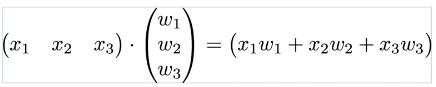
• H(x) = w₁x₁ + w₂x₂ + w₃x₃

행렬을 통해 표현하면 x가 몇 개든간에 X라는 변수 하나와 W라는 변수 하나로 표현할 수 있게 됩니다.

전체 훈련 데이터에서 셀 수 있는 1개의 단위를 샘플(sample)이라고 합니다. 각 샘플에서 y를 결정하게 하는 독립 변수(x) 하나하나를 특성(feature)라고 합니다. X 변수를 정의할 때 (샘플의 수 x 특성의 수)를 사용합니다. 원본 예시에서 Quiz 1, 2, 3과 5개의 샘플 데이터가 있다면 흔히 (5 x 3) 아래 이미지처럼 표현 가능합니다. 여기에 가중치(w)를 곱하고 편향을 추가하면 X, W, B변수 3개로 다중 선형 회귀의 가설 연산을 표현 가능합니다.

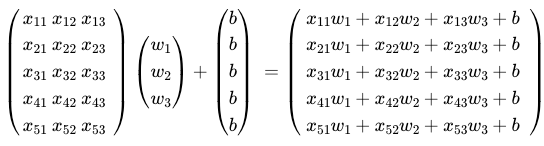
예시는 다음과 같습니다.

# 샘플 데이터
x_train  =  torch.FloatTensor([[73,  80,  75], 
                               [93,  88,  93], 
                               [89,  91,  80], 
                               [96,  98,  100],   
                               [73,  66,  70]])  
y_train  =  torch.FloatTensor([[152],  [185],  [180],  [196],  [142]])

# 가중치와 편향 선언
W = torch.zeros((3, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)

optimizer = optim.SGD([W, b], lr=1e-5)

곱셈은 다음과 같습니다. 다만 곱셈 좌측의 행렬 열 크기와 곱셈 우측 행렬 행 크기가 일치해야 합니다.

• (5×3) @ (3×1) = (5×1) → matmul

hypothesis = x_train.matmul(W) + b

이후의 계산은 선형 회귀와 동일합니다.

# H(x) 계산
hypothesis = x_train.matmul(W) + b

# cost 계산(오차)
cost = torch.mean((hypothesis - y_train) ** 2)

# cost로 H(x) 개선
optimizer.zero_grad() # -> 현재 기울기 초기화
cost.backward() # -> 오차를 미분해서 기울기 계산
optimizer.step() # -> W, b 업데이트

다중 선형 회귀 한계점

다중 선형 회귀 역시 한계점이 존재합니다. 만약 두 개의 독립 변수 x1, x2가 같이 움직인다면 둘 중 뭐가 진짜 영향을 주는 건지 구분하지 못하는 다중공선성 문제가 발생합니다.

또한 비선형 관계를 표현 할 수 없어 곡선이거나 복잡한 패턴이면 정확한 예측에 한계가 존재합니다.